THE WORLD'S BEST TUNING LEVER...
BY SCHAFF

This is the best tuning lever we can find anywhere.  If you
intend to make any kind of career of tuning pianos, this tool
will be a great help.  It is not just classy though.  There are
many tool attachments which can be added to the lever to
make it useful in all sorts of applications.  You may eliminate
buying a special tool by simply buying the appropriate
attachment, later on when you need it. If you have a Hale
lever, the thread pattern for the head to the shaft, and the
tip to the head, is the same. These attachments should fit
your Hale lever.

Definition: A "Tuning Lever" and "Tuning Hammer" are the same thing.

YOU CAN NOW ORDER BY PHONE

         Best in the trade!!!
Schaff Premium Tuning Levers    

Hand machined of the best alloys.

Accepts a vast assortment of attachments and tips...
To enhance the tool over the years.  
"Extension" means that the handle can be
         lengthened considerably. 
Rosewood handle--  Sigh!!!!  
Packed in a fleece lined pouch-- What else?

Take it to the country club and flash it at the piano
         man  :-)
I hate to admit this, but some musicians look for this
tool to see if you are a serious tuner.  If you are just
beginning, flash the lever and act like the silent
type--  You never know, it might get you into a
concert hall. 

In most cases, the lever is drop shipped directly from
the manufacturer to you. Any problems are quickly resolved.

EXTENSION MODELS

First Quality Rosewood Extension Lever
        Fine piano stores have one of these.  
        Leave it on a tuning pin hanging out in space, and it says,
        "This guy is keeping on top of his pianos."
        Jerry Peterson in Grand Rapids always had his hanging there
        on a tuning pin on a big black Yamaha.  
        Hubris abounds folks, and admit it-- We love a little class, right?
        
        Overall length is 11-1/2 inches with a possible 6-1/2 inch
        extension Comes with a #2 star tip, Part Number 14B, and 13G head 

        Part Number                                                      SH21
        Price                                                                 $ 375.00

        Replacement 8 inch long extension shaft-- Threaded on both ends

        Part Number                                                      SH21R
        Price                                                                  $ 41.75

The Black Nylon Handle Extension Lever
       Same Extension Tuning Lever as SH21, but with
       Black Nylon handle- Actually, this is very practical
       since the nylon will not react with hand moisture.
       8 inch handle, 11 1/2 inches overall-- weighs 18 oz.
       Comes with a 14B #2 star tip and 13B head.
     (Does not include tip wrench & carrying case.)   

       Part Number                                                        SH16
       Price                                                                  $ 299.00

NON-EXTENSION MODELS

(NOTE: We do have the newest in Carbon Fiber Tuning Levers. They are a custom-assembled item. Contact us for details.)

Piano Factory Style Tuning Lever
          This lever is designed for factory work. It is great
          for installing new tuning pins. With the pin plank in
          place and supported beneath, you can turn in a tuning
          pin a couple of turns, then hammer on the butt end of
          the tuning lever head with a hammer and drive in the
          pin all the way. 13" long with #2 tip- 15 ounces. Great
          for driving loose pins in deeper in uprights while tuning.
        Part Number                                                        SH18
        Price                                                                   $ 79.00

Black Nylon Handle
          An alternative to wood. Has a stationary handle made of
          black nylon with a light swirl grain. 8 inch handle.
          12 inches long overall.
          Comes with a #2 star tip and a 13G head.
        Part Number                                                        SH4
        Price                                                                  $ 145.00

Deluxe Professional Lever with Rosewood Handle

         This lever is one of the most classy looking levers I have seen.
         It is made on the design of a lever made long ago, and it blends
         the beauty of chrime, brass, and Rosewood. This lever also gives
         you the option of changing heads and tips like the quality levers
         above This lever has the same quality of steel of the #21 above, but
         the shaft is not extendable. Overall length is 11-1/2 inches long.
         8 inch rosewood handle. Comes with 13G head and #2 star tip.
         Part Number                                                 SH6
         Price                                                              $ 249.95

         Substitutions For Tips and Heads
         Custom head and tip choices can be arranged, but some price increase
         must be expected.  See below for options galore.

Are these levers beyond you means?
Check out our Apprentice, and Craftsman Levers.

Schaff attachments for the above Tuning Levers:  
         All parts below will fit models above.

Part Description:                                                                                                          Part Number        Price

       

Hale and Schaff Tuning Lever Heads

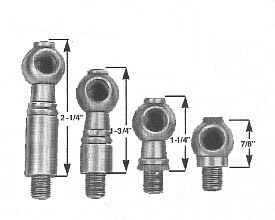
Medium 1 3/4" head at 5 degree angle         SH13H               $ 54.00
Medium 1 3/4" head at 15 degree angle       SH13H-15         $ 54.00
Short 1 1/4" head at 5 degree angle             SH13G               $ 34.00
Short 1 1/4" head at 15 degree angle           SH13G-15          $ 49.75
Extra Short 7/8" head at 15 degree angle     SH13F                $ 42.00
Long 2-1/4" head at 5 degrees angle            SH13J                $ 56.00
Long 3" head at 5 degrees angle                  SH13K               $ 61.75
Long 5" head at 5 degrees angle                  SH13L                $ 65.00

Tuning Lever Tips
These tips screw onto the head only

Small Star Number 1                                                                                                           SH14A                 $ 22.50
Standard Star Number 2                                                                                                     SH14B                  $ 22.50
Large Star Number 3                                                                                                           SH14C                 $ 22.50
Large Star Number 4 (not shown)                                                                                        SH14G                 $ 24.00
Square Number 2 size only                                                                                                   SH15                   $ 23.50
Oblong (For square Grands mostly)                                                                                     SH3128                $ 28.75

Schaff One Piece Tuning Lever Head / Tip Combination
Cannot be used with other tips.

2-1/2 inch long, #2 star head, 5 degree angle                                                                         SH17                    $ 28.75 
2-1/2 inch long, #3 star head, 5 degree angle                                                                         SH17-3                 $ 28.50
2-1/2 inch long, #2 star head, 15 degree angle                                                                       SH17-15               $ 28.50
1-1/2 inch long, #2 star head, 15 degree angle                                                                       SH17A                  $ 28.50
4 inch long, #2 star head, 5 degree angle                                                                                SH17B                  $ 33.75
5 inch long, #2 star head, 5 degree angle                                                                                SH17C                  $ 37.50

Misc. Accessories

Fendon thin walled head/tip combo
This is now the option. Fits all levers with made by Schaff and is styled like a Hale head
Has a 2-1/2 inch length, #2 star tip. Screws onto the shaft of a high end lever. Chromed.
CAUTION: This tip is only for where tuning pins are too close together, or where
a pin is set close to the brace on a grand. It is not able to be used continuously due
to the thin walls of the tool.                                                                                                    SH17N          $ 31.00

Thin walled tip- (Not shown)
        For use where pins are very close together or where a pin is too close to the harp                                                                                                          
        1-1/2 inches long                                                                                                          SH14H            $ 30.00

Tip Wrench--  Removes tips easily                                                                                       SH11             $ 17.45

ORDER BY PHONE WITH CREDIT CARD
CALL TOLL FREE: (800) 338-8863
If there is no answer, please leave a message- we do answer our voicemail

OR:
Go to Mail Order Form for printing:

Online help available

BACK TO PIANO TITLE PAGE

Chapter IV. PRACTICAL TUNING IN EQUAL TEMPERAMENT.

After all the discussion that has gone before, we have now to see how we may put our ideas into practice. It is plain from what has been already said that Equal Temperament is a perfectly simple system and one admirably adapted to present ideas and methods in musical composition and the making of musical instruments. Until there comes that change in public taste which demands something finer, we shall have tempered pianos, tempered orchestras and tempered intonation generally; with our ears more and more becoming used to tempered sounds and unused to pure sounds. It is therefore highly important not only that the tuner should be thoroughly capable of doing the very best work in temperament that can be done, but also that he should make it his business to realize every day and every hour that the work he is doing is in reality a compromise with truth; necessary no doubt, but a compromise just the same ; and one which exists solely because instruments, musicians, and the public alike are unready for anything better.

Recognizing Just Sounds.

In the circumstances and considering the inherent difficulty of tempering accurately by estimation of ear, I most earnestly advise every student to practice the tuning of pure Fifths, Fourths, and Thirds. Unisons and octaves must be tuned pure anyhow, but most tuners, in common with virtually everybody else, are familiar only with the tempered form of the other intervals and never dream of asking how they sound when purely intoned. But in order to recognize with any sort of accuracy the number of beats per second that a tempered interval is generating, it is absolutely essential that one should be acquainted with the true condition of that interval ; familiar with its sound when evoked in purity. Thus I would counsel every reader of this book to form the habit of always tuning all intervals pure and hearing them satisfactorily as such, before attempting to temper them ; and also to get into the equally valuable habit of tuning, for his own amusement and satisfaction, series of pure chords on the piano; which of course can be done, so as to be satisfactory for one tonality and even capable of being played in to that extent.

Measure of Purity.

The measure of purity is the absence of beats. If intervals whose ratios of frequency are such as to avoid alternation in phase-relations¹ are tuned on any instrument with absolute accuracy, there will be no beats between them. (I here purposely have omitted reference to the “beat-tones,” otherwise known as resultant or combinational tones, which are in reality generated by very rapidly moving beats from high coincident partials in intervals that otherwise would have no beats ; but these beat-tones are true musical sounds and for the tuner's purpose need not be considered in the present discussion; especially as they are almost imperceptible on the piano.² The fact, then, that no beats are heard is a test quite accurate ; and the work of tuning is immensely facilitated if the tuner is able to assure himself when a condition of beatlessness exists, instead of always being vague on this point.

Unison Tuning.

The acquirement of a cultivated ear for purity of interval cannot better be begun than by learning to tune unisons correctly. Considering also that tuning of unisons comprises about two-thirds of the work of tuning a piano, since most of the tones are triple, and nearly all the rest double, strung, it will be seen that this important part of the tuner's work deserves the most careful attention. It is fortunate that the unison is the simplest of intervals to comprehend and to appreciate aurally. It is requisite in beginning the study of tuning to ascertain with complete certainty the peculiarities of beats. Two tuning forks tuned in unison and with one then slightly loaded with a minute piece of wax, or other material, afford a simple and easy experiment in beat production.¹ It will be useful to begin by making such an experiment and listening carefully to the beats until the peculiar rise and fall of the sound is so plain that it can never again be mistaken. The opposite experiment, made by removing the load and returning the forks to complete unison, presents the sound of a perfect unison, with complete absence of beats. It is also, by the way, interest ing as providing an almost perfect form of simple vibration, without partials.

To tune two piano strings in unison is not a very difficult task if it be gone about rightly. In the first place, it is well to listen carefully to the work of a professional tuner, when the opportunity occurs, with the object of noting by ear how he adjusts his unisons. A little practice will enable one to hear instantly the difference between the beating tone of two strings which are out of tune with each other and the pure continuous beatless sensation of tone developed when the unison is perfected. Having once obtained some facility in thus cultivating the hearing, the student may obtain a tuning hammer and attempt to do some practical adjustment of unisons.

Argument concerning the manipulation of the hammer would at this stage be out of place, I feel, for it would tend rather to confuse than to assist the student.² Let me then simply say that the tuning hammer is to be placed on a tuning-pin corresponding with one string of a triple unison. Let one string of the triple unison be damped off, leaving two to sound when the piano digital is struck. If the piano has not been tuned recently the student will undoubtedly hear beats; and if these are not distinct or frequent enough, let the tension on the string be relaxed by turning the pin slightly toward the left or bass end of the piano. Now, let the reverse operation be undertaken, and the hammer turned back towards the operator, thus gradually tightening up the string again. As this is done it will be observed, if the digital is repeatedly struck, that the beats, which at first we may suppose to have been quite frequent, become slower and slower, until if the string be rightly tuned, they disappear altogether, leaving a pure continuous uninterrupted sound.

Practice.

In beginning the work of learning to tune pianos, it is advisable to practice for some time in bursts of from fifteen to thirty minutes each, on simple adjustment of unisons. The manipulation of the hammer, of which I speak at length in the next chapter, now, of course, begins to claim attention ; but for the present it is enough to say that the pin must be turned without wrenching its outer end and without pulling downwards on it. It is advisable to rest the arm and keep the handle of the tuning hammer nearly vertical.

It will then be advisable to undertake settling the unisons of an entire piano, and not until this has been accomplished is the student fit to take the next step. It will be observed that whereas the middle strings afford a comparatively simple task, those of very low and very high frequencies alike are more and more elusive; and careful practice and listening are required before they can be mastered. The measure of purity, be it remembered, is absence of beats; and so long as beats can be heard the unison is not pure.

Octave Tuning.

The Octave is the unison transposed. Hence Octave tuning is just as simple as unison tuning, in principle, and almost the same in detail. The beats arising in a two-string unison are between the fundamentals of two sounds whilst in an Octave the beats are between the 1st partial of the higher and the 2nd of the lower ; the Octave proportion being 1 : 2 and the coincident partials therefore being Nos, 2 and 1 respectively.¹ Thus throughout the entire middle portion of the piano anyhow, there will be very little difficulty in tuning Octaves, once the student has learned to adjust the unisons accurately, for exactly the same beats are heard and the same blending of the beats into a condition of beatlessness, as the Octave is perfected, until a perfect , Octave is almost as complete a blend of sound as an unison.

Exact Tests.

In certain regions of the Piano it is quite impossible to obtain certainty of Octave tuning merely by estimating the extinction of beats between the two members of the interval. In the low bass particularly, the coarseness of the strings and the almost inevitable impurity of their intonation lead to the generation of all kinds of false beats which confuse the student and are a source of annoyance and inaccuracy even to the expert. The student should of course practice tuning Octaves throughout the entire compass, but he will find that in the low bass he must have some test for accuracy better than afforded by aural comparison of the two members of the interval. Fortunately, other tests are available, and each is capable of giving highly correct results.

The Octave comprises a Fourth and a Fifth in succession. A Fourth above Co runs to Fg and a Fifth from that runs from Fo to C3. If now, whilst tuning the octave Co — C:j (say) we sound the Fourth G^—F^ and then the Fifth Fg— C3, and find the beats in the Fourth equal in number to the beats in the Fifth, the Octave is tuned accurately. This is so because all Fourths and Fifths in Equal Temperament are distorted slightly so that the coincident partials are actually a little distorted also. In the present case, the coincident partial is C4, the 4th partial of C2, the 3rd of F2 and the 2nd of C3.

The first octave test therefore is made by ascertaining the number of beats between the Fourth above the lower sound and comparing these with the beats in the Fifth below the upper sound. If the beats are the same in number, then the octave is perfect. But, if the test is made between lower Fifth and upper Fourth, then the upper Fourth will beat twice as fast as the lower Fifth.

Minor 3rd and major 6th.

For the lower regions of the piano especially, but useful everywhere, is the test of the ascending minor Third and descending major Sixth. If we are tuning, for instance, from C₂ to C₃, we try the minor Third C₂ — E flat₂ and note its beat-rate. Then we try the major Sixth E flat₂ — C₃ and try its beats. If the beats in the two cases are equal in rate, then the octave is tuned accurately.It will be observed that this is the same idea set forth in the previous paragraph. The E flat is the common tone, and the minor Third and major Sixth are complementary. The coincident partial is the 6th of C₂, the 5th of E flat₂ and the 3rd of C₃=G₄. But if the Sixth be the lower and the Third the upper, complementary intervals used, the Third will beat twice as fast as the Sixth.

Beat rates in Thirds and Sixths.

It is well to note in passing that as shown in the tables in Chapter III (supra), the beats in. Thirds and Sixths, major and minor, are considerably faster than in Fourths and Fifths ; and the student after tuning an octave may profitably examine the complementary Thirds and Sixths within that interval for the purpose of studying their beat rates.

The Tenth test.

A Tenth is an Octave plus a major Third. A good octave test is to be found here also by using the major under-Third and Tenth. If tuning C₂ to C₃, test by the major under-Third C₂— A flat₁ as compared with the Tenth A flat₁ — C₃. The coincident partial is the 5th of A flat₁, the 4th of C₂ and the 2nd of C₃,=C₄. This test is useful throughout the entire compass and especially in the lower registers.

Observe that beat-rates, as shown by Table III (Chapter III), vary as the frequencies of their generators, so that the nearer we approach the lower bass, the slower are all the beat-rates. In fact, the beat of the Fourths and Fifths cannot be distinguished at all in the lower bass, and we have to depend on Thirds and Sixths, It is very important of course, to know how many beats in a second any given interval should have ; and Table III supplies this requisite.

Counting Beats.

The tuner, for practical purposes, must count his beats by mere aural estimation. The result is never perfectly accurate. It is, however, the only method that can be used in practical work, and the method, therefore, that we must develop to the highest possible degree of excellence. In the first place it will be noted that Table III (Chapter III) gives the beat-rates accurate only to within .5 of a beat per second. This is simply because, although the error is mathematically large, the human ear, at least with the evanescent tones of the piano, cannot judge any more delicately, and even then needs practice and patience. It will usually be found that for accurate work beat-rates of from 2 to 5 per second are most easily counted. Above this is difficult; below it is equally so. Beats of less than 1 per second rate are hard to hear and keep track of. However, the tuner may accustom himself to estimating beat-rates by one or two simple methods.

Seconds' Watch.

Watches are usually provided with seconds' hands and these usually make four ticks per second. By listening carefully for say ten minutes at a time, the student can soon learn to hear accurately a beat-rate of 4 per second. But the precise tick-rate of one's own watch must be accurately determined.

Pendulum Clock.

Pendulum clocks of the large sort often have very slow swinging pendulums. These sometimes produce one complete to and fro swing (complete vibration) per second.

Pendulum.

Ellis suggests (App. 20 to Helmholtz) , that the student may make himself a pendulum from a piece of string and a curtain ring, with provision for shortening or lengthening the string readily. Now, for counting during any length of time, as for instance 5 seconds, which is a useful unit of time in counting beats of the piano, we may arrange the length of the string as shown below :

It is important to note the manner of measuring, as above.

These three beat rates are very important, especially the first and third, in the practical work of tuning.

Other methods may suggest themselves to the student. The perforated rotating disk to be found in every high school physical laboratory can be used also to give series of taps (by holding a card against a circle of the perforations while the disk is rotated), of any required speed.¹

Of course the point is that the tuner ought not to trust to guess work but should try to know when he hears a beat-rate what it really is. He can learn to do this; and learn easily. By watching and counting the swings of a pendulum such as that described above he can soon learn to feel the rate of swing; which is an exceedingly valuable accomplishment and one easy to acquire. Certainly, it is impossible without some such training ever really to do distinguished work in the most important and most difficult branch of tuning pianos; that which is called “laying the bearings,” and which we must now consider.

Laying the Bearings.

The scheme already laid out (Chapter III, supra), for tuning the central octave in Fourths and Fifths forms the basis of the explanations now to be made: Reproducing this in type and appending the beat rate as ascertained for each interval from Table III and the frequency as given in Table I, we get Table IV.

There are two observations to be made immediately. The first is that although the Table shows 36 steps, only 13 notes are actually tuned, and the remaining steps show tests made by intervals and chords generated during the progress of the tuning. These test intervals and chords are of the utmost importance, just as important as any other element of the work, inasmuch as they afford a complete measure of the correctness of the tuner's progress. But the actual tuning is confined to the series of Fourths and Fifths shown.

The second is that to count beats at something very close to these rates is not impossible by any means. I counsel the student to realize that any definite method like this has the inestimable advantage of being founded on fact. What is more to the. point, such a method leads to that much closer accuracy which should distinguish masters of the art.

Variations in pitch for practical tuning.

The figures given are sufficiently accurate for any pitch between C 258.65 and C 264, which range covers the common variations as found in modern pianos. In strict fact, any rise in pitch above the International C 258.65 involves a progressive rise in beat-rate. But the amount of increase is too small for practical purposes; usually at least.

Importance of Accuracy.

Of course I cannot too strongly urge the importance of accuracy, of not being content to do things fairly well or even reasonably well; but of insisting to the utmost upon the possibility of doing ever and ever more accurate, more scientific and more complete, work. Tables III and IV do represent the utmost in accuracy, probably; and the figures given in these Tables can be attained by those who will practice the Art of Tuning with patient devotion. The Artist will attain them. May every reader of this book earnestly strive for that perfection.

Methods of Using Tests.

The test Thirds and Sixths, and the test triads are to be used constantly throughout the work. Observe carefully the rise in beat-rate of the ascending Thirds and Sixths. This rise must be accurately measured. It will be found, of course, that the beat-rate doubles in each octave and the extreme Thirds should show this progress. No better test of the accuracy of the bearings can be found. It is not sufficient to “come out right,” by which is meant, to arrive at the last step and find the final octave reasonably clear. It is necessary that every step should be right. This means care, patience, study; which lead to mastery.

Tuning from the Bearings.

From the Bearings the tuning proceeds by octaves and unisons according to the methods laid down and explained in the earlier part of this chapter. The student is again warned to look out that his octave tuning does not begin to slide off from accuracy by the accumulation of imperceptible into intolerable errors; and to this end the constant use of the various tests already explained, as well as of double octaves and triads, is recommended.

Obtaining required Temperament in intervals.

Lastly, let me say again that the only way to tune intervals so that their beat-rates are reasonably accurate is first to tune them pure and then to make the necessary correction up or down. It is impossible in any other way to acquire true delicacy of ear. No other method will produce the required results. This is an immensely important truth and covers one of the most neglected elements in the art. The rule of tuning all intervals pure before proceeding to temper, is essential ; and the student ought early to achieve this habit. The mere fact that Equal Temperament is an artificial mathematical compromise, should in itself be sufficient to persuade the tuner that this view is sound, especially when the reasons adduced at the beginning of this chapter are recalled. Until one knows practically the true beauties of Pure Intonation, the almost equally strong virtues and vices of Equal Temperament will in neither case be duly appreciated. Any one who has had the privilege of listening to a first-rate string quartet or to a really good unaccompanied chorus, will understand why pure intonation, once recognized, is ever after treasured in memory.