PIANO WIRE OR STRING- Piano wire and strings

Bass strings can need replacing for two main reasons. Obviously,
if they break, they need replacing. But, bass strings can also go dull.
After turning them, they may still sound bad, and they may develop
overtones. The answer is to either replace them one at a time, or do
only the worst offenders. When restoring a piano, ALL strings should
be replaced in order to get the original sound back.

YOU CAN NOW ORDER BY PHONE

BASS WIRE (Strings)

If your wire to be replaced appears to made of gray iron metal, it probably is.
This is no longer used in the trade because it rusts too easily, and it goes dull
with age. We send only copper wrapped wire.

We now offer many more options than in the past, so if you came here in the past
and wished you had more choices, browse again pleas.

CAVEAT EMPTOR:
When replacing a bass string on an old piano, it is virtually impossible
to us to duplicate the timbre and sound quality of your old strings in the
area of the string you wish to replace. If this bothers you, then you need
to find your strings at some other supplier. We will not replace a string
simply because you don't like the sound quality. Your old strings are
aged and do not react and vibrate like new steel and copper. If you
understand this, then we will do our best to get close.

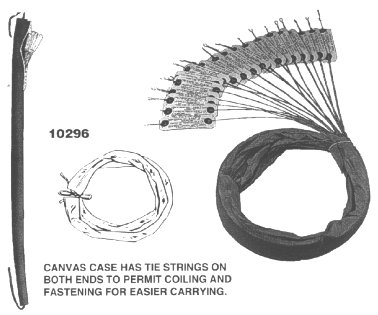These strings permit you to make on the spot replacement of strings that break, except on the largest concert grands. You simply unwind the copper winding to match the broken string, and install it. The core of universal strings is hexagonal, so when you remove copper winding, you simply crimp the end of the winding a bit, and the core wire holds the winding in place. You will find that an exact duplication will result in a more perfect sound after some time passes. These universal strings are avoided on concert and performance pianos if the customer can afford the exact duplicated strings. The universal strings also have the advantage of being quick to order from us or the suppliers.

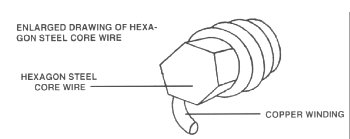
The purest sound is assumed to come from a hand made string fitted to your particular piano.
But the universal string can at least fill in until a string made for the piano can be ordered.
The universal string will also save a concert if the tuner is on hand and has strings with him.

Single universal string $ 39.00 each
See Universal String Chart below for broken bass string.

Packet of 37 strings-- S50 strings
For better quality grands that use a lighter core wire SH2037 $ 450.00

Packet of 10 strings-- S50 strings
Very heavy for Steinway Grands and other monsters SH2010 $ 250.00

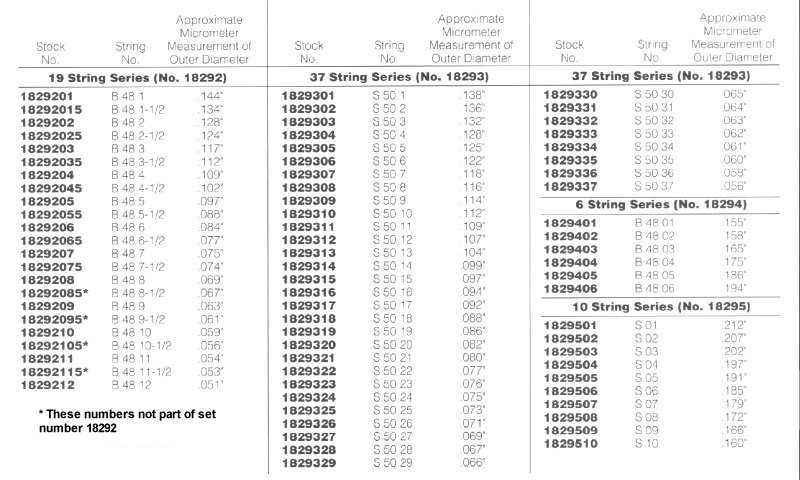
UNIVERSAL STRING CHART: The following chart gives the order number on the left.
The String Number is the piano trade standard size for the string. On the right is the micrometer size in thousandths.

Why duplicate strings? All strings below are made on a lathe and hand controlled by craftsmen who do this
for a living. The core is not six sided as with Universal Strings above, and the sound is the best. A universal
string is a very legitimate choice when one string breaks. When rebuilding, only duplicated strings should
be used to get the best results.

When ordering sets of bass strings made to order it is always helpful if the manufacturer's name and serial number of the piano is given. Be aware that the brand name (such as Baldwin, Kimball, Aeolian, etc) may not be the same as the trade name on the fall board. Try to find the actual company name under the lid or on the harp. This information is very useful even if the strings or a pattern are sent. Production time can be reduced considerably if the string maker can refer to his personal file and notes on various brands of pianos.

Be very cautious in letting off the tension on a piano to replace strings. Loosen ALL strings in the whole scale in several steps to avoid breaking the harp. Do not take off the bass strings and not loosen tension on the treble. Let off the treble also at least to the point that the treble strings sound very dull when plucked.

For sets of strings up to 60 inches in length-- SH2044 $ 15.00 per string
Concert Grands and Square Grands-- SH2045 $ 16.50 per string

10 to 20 consecutive single wound strings SH2042 $ 22.00 per string
8 to 20 consecutive double wound strings SH2043 $ 23.00 per string

SHIPPING OF FULL SETS OF STRING.
   Shipping-- $ 30.00 to the Midwest USA
   Shipping-- $ 40.00 to the West Coast, Deep South, Southwest, and upper New England, USA
   This price reflects our shipping to our supplier and their shipping to you by UPS.

PRICE:
Single Wound   Part Number 2040   $ 37.00
Double Wound Part Number 2041    $ 40.00
Yamaha Strings Part Number 2047 $ 45.00
   Shipping-- $ 12.00 via Priority Mail

Canvas Case for carrying universal Strings-- 72 inches long
Whatever you do, keep your piano strings DRY.
See case in graphic at top of page SH2007 $ 65.00

ORDER BY PHONE WITH CREDIT CARD
CALL TOLL FREE: (800) 338-8863
If there is no answer, please leave a message- we do answer our voicemail

Online help available

Chapter II. ON THE VIBRATION OF A PIANO STRING. (TABLE OF CONTENTS)

Of all sounding bodies known to music, the musical string is without doubt the most common, the most easily manipulated for musical and mechanical purposes, and the most efficient. Acquaintance with ascertained facts as to the behavior of musical strings under practical conditions is necessary for the complete equipment of the piano tuner; although this acquaintance need not be exhaustive, so long as it be, to its extent, exact. Avoiding mathematical symbols which, requisite as they are to a comprehensive study of Acoustics, may nevertheless be beyond the familiarity of most of those who will read this book, I shall here briefly investigate certain properties of musical strings and especially of the piano string. The discussion, I can promise, need seem neither dry nor uninteresting.

To be exact, a string should be defined as a perfectly flexible and perfectly uniform filament of solid material stretched between two fixed points. But such a string, it must be observed, can exist only as a mathematical abstraction, since neither perfect uniformity nor perfect flexibility can be expected in strings made by human hands. A string of given flexibility becomes more flexible, as to its whole length, if that length be increased, and, conversely, stiffer as its length is decreased. The property of weight also fluctuates in the same way. Likewise if the force whereby a given string is stretched between two points be measured in a given number of pounds, the effective tension equivalent thereto will of course be decreased if the string be lengthened; or conversely will be increased if the string be shortened. A string 12 inches long stretched with a weight of 10 pounds is subjected to a lower tension than is a 6-inch string of similar density and thickness stretched with the same weight. These allowances and corrections, obvious as they are, must constantly be kept in mind if we are to understand the behavior of practical strings, since all the acoustical laws which govern such behavior must be modified in practice according to the facts disclosed above.

We have learned that musical sounds owe their existence to the fact that some solid body is thrown into a state of periodic vibration. The kind of vibration can best be explained by likening it to the swing to and fro of a pendulum. A pendulum is fixed at one end and tends naturally to swing back and forth on its pivot. The kind of vibration which the pendulum performs is called simple or pendular vibration. The tuning fork, when set in vibration, is also very much the same thing as a pendulum, since one end of each prong is fixed and the other end can therefore swing freely. The tuning fork furnishes, when excited, an excellent practical example of simple or pendular vibration of sufficient rapidity to produce musical sound.

Go to a piano and strike one of the low bass keys in the octave between A-₁ and A. These very low keys operate on single strings only and hence are excellently adapted for our purpose.¹ Strike on the piano the key (say) F. Hold the key down, and listen carefully. At first you will hear simply the full sonorous tone F, deep and solemn. But listen closely, repeating the experiment till the ear becomes familiar, and you will gradually observe that, mingled with the original sound F, there are a number of other sounds, apparently very closely related to the original, coloring it rather than altering its pitch, but at the same time recognizable as sounds that spring from a different level. By repeating the experiment with various of these low strings (or by going higher and taking care that one string in the two-string unisons is damped off), you will gradually be able to perceive the remarkable fact that every piano string produces a sort of compound tone, consisting primarily of its natural tone or fundamental, as we may call it, but containing also the octave thereto, the fifth above that and the second octave. It is true that these extra sounds are feeble and can be heard only by means of practice and the exercise of patience; but heard they can be, more and more clearly as one's familiarity with the process grows.

The truth is that the piano string does not evolve a simple but an exceedingly complex musical tone. Not only the three extra tones of which I spoke before can be proved to exist, but in fact an immense number of other tones, all bearing given harmonic relations to the fundamental, can be shown to be evoked, and by the use of suitable apparatus can be detected and isolated, one by one, through the sense of hearing. Special resonators have been made which enable the hearer to detect these partial tones clearly. Even without such special apparatus, however, we can detect a number of the partial tones if we take advantage of the piano 's property of sympathetic resonance; a property imparted by the sound-board.

Hold down the middle C key, without striking the string. Then, while holding the key down, strike a powerful blow on the C immediately below. When the sound has swelled up, let go the lower key whilst holding on to the upper or silently pressed key. At once the sound of middle C floats out of the silence, pure and ethereal. What is the cause of this sound? How has the middle C string been excited? The answer is found in the fact that the lower string which was struck, not only produces its fundamental tone but also evokes its octave above. The peculiar sort of vibration of the C₂ string which produced this octave is resonated through the sound-board and reproduced on the middle-C string. In the same way, the twelfth (G₃) can be brought out, and so can the next octave C_4. In fact, with a very good piano and by choosing a low enough sound for the fundamental, even higher partial tones can thus be brought out by sympathetic resonance from the original string to the string corresponding with the true pitch of that partial.¹

Thus we learn that the piano string vibrates as a complex of vibrations, not as one simple form of vibration; for it is evident that if the string evokes, as we know it does, a complex of sounds, these must arise from a complex of vibrations. Let us see how this is :

Turning again to the piano, select a string in such a position that it can be measured accurately as to its speaking length. A grand piano is most convenient for the purpose, and the string may be selected from the overstrung or bass section. Now accurately measure the speaking length of the string between bridges, and mark carefully with a piece of chalk on the sound-board the exact middle point as near as you can determine it. Then sound the string and whilst holding down the key, touch the string at the middle point very lightly with a feather. If you perform the operation skillfully enough, you will find that instantly the fundamental tone of the string ceases and there floats out the octave above, quite alone and distinct. Measure now one-third of the length, mark it, and again sound the string. Placing the feather carefully at the exact division point and damping the shorter segment with a finger, the fifth above the original sound is heard.

What is the meaning of all this? Plainly in the first case it meant that the string naturally subdivides itself into two parts of equal length and that the vibration of either half gives the octave above the original. Thus we have two vitally important facts at our disposal, one relating to the form of vibration of the string and the other to the law of string length as proportioned to pitch. Moreover, in the second case, if we allowed the 1/3 division of the string to vibrate, we should get from it a sound an octave above the sound of the longer or 2/3 division. Since we damped the shorter segment, however, we conclude that the fifth above the original sound was produced by a string length 2/3 of the original length. If we now continue our experiments we may find that 4/5 of the original length produces a major 3rd above the original sound, and that 1/4 of the length produces a sound 2 octaves above the original sound. Plainly then, we have two great laws revealed.

When a string fixed at each end like the piano string, is struck at one end, it vibrates in a complex form, most strongly in its full length but also perceptibly in segments of that length such as 1/2, 1/3, 1/4, and 1/5.

The pitch of a string — that is to say, the number of vibrations, per unit of time, it can perform, is proportional inversely to its length. Thus, since an octave above a given sound has twice as many vibrations per second as the original sound, it follows that to obtain a sound an octave above a given sound we must have a string one-half as long.

Similar laws exist with regard to the influence upon string vibrations of weight, thickness and tension. Without undertaking to prove these completely, we may state them briefly as follows :

The frequency of a string's vibration is inversely proportional to the square root of its weight. In other words, if the weight be divided by 4 (the square of 2) the frequency will be multiplied by 2. To produce a tone one octave below its original tone, the weight of the string must be increased in the proportion 4:1. To produce a tone one octave above the original tone, the weight of the string must be only 1/4 its original weight.

The frequency of string vibrations is directly proportional to the square root of their tension. In other words, to get twice as many vibrations, you must multiply the tension by 2² = 4. To get four times as many vibrations you must multiply the tension by 4² = 16. So if a string be stretched with a weight of 10 lbs. and it is desired to make it sound an octave higher, this can be done by making the stretching weight (4 X 10)= 40 lbs.

The frequency of string vibrations is inversely proportional to the thickness of the string. If a string of a given length and weight produces a tone of a given number of vibrations, a string of the same length and twice the thickness will give a tone one octave lower; that is, of half the number of vibrations.

All of these laws, be it remembered, are based on the assumption of mathematical strings, in which weight and stiffness remain constant through all changes in length. In the case of the actual piano string, in which the weight and tension do vary with the length, some compensation must be made when calculating. Thus, to illustrate, it is found that whereas the acoustical law for frequency of vibration requires a doubling of the string length at each octave downwards or halving at each octave upwards, the practical string, where weight and tension vary with length, requires a proportion of 1:1.875 instead of 1:2. This difference must be kept in mind.¹

Before, however, we go on to consider the influence exerted, through the peculiar manner in which strings vibrate, upon the problems of tuning and tone-quality, we must take the trouble to discover why they should, in fact, vibrate in this rather than in some other way. It is easy to talk about string subdivision and partial tones, but there is very little use in mouthing words that do not carry with them to our minds real meanings, or in talking about processes which we do not really understand. So, let us take the trouble to discover why a string vibrates as we have shown it to vibrate. Here again, the piano shall be our instrument of investigation.

The first thing to realize when we begin to talk about string vibrations is that the vibration itself is merely the transmission of a motion from one end of the string to the other. This motion will continue until it is transformed into some other sort of energy or else is thrown out of its direction into another direction. Suppose that you take a long cord, like a wash-line. Obtain one as much as twenty feet long. Fasten one end to a post and stretch the cord out until you hold the other end in your hand with the entire length fairly slack. Now try to jerk the cord up and down so that you can get it to vibrate in one long pulse. That pulse will affect the entire length of the cord, which you will observe to rise from its plane of rest, belly out in a sort of wave, descend to the point of rest again, belly out once more on the opposite side and return to the point of rest, making a complete swing to and fro. Compare the illustration figure 6.

When you find that you can do this (practice is needed), try a different experiment. Try to jerk the cord with a sort of short sharp jerk so that, instead of vibrating in its whole length, a sort of hump is formed on the cord which travels like a wave through a body of water. This short wave will travel along the whole cord, as you will be able to see by watching it narrowly, until it comes to the end fixed on the post. At once you will see that the wave, instead of disappearing, is reflected back, reversing its direction of travel and also its position, being now on the opposite side of the cord. Thus reflected, the short wave travels back to you. This is an example of what is called the reflection of a sound impulse. But it has a very important bearing on the general problem of piano string vibration, as we shall see.

Suppose that you are able to time your efforts so carefully that you can deliver a series of these short sharp jerks, forming these short waves, at the rate of one per second. If you time your impulses carefully, you will find that the second impulse will start away from your hand just as the first impulse starts back from the fixed end of the string. The two impulses, traveling in opposite directions and in opposite phases of motion (in positions on the cord opposite to each other), will meet precisely in the center, for neither one can pass the other. At their meeting place, the exact middle of the string, the forces are equal and opposite, so that a node or point of greatly diminished amplitude of motion is formed. The two pulses therefore have no option but to continue vibrating independently, thus dividing the string into two independently vibrating halves, each of double the original speed. See the illustration figure 7. Meanwhile a second impulse from the hand begins to travel along the cord and upon its meeting the already segmented halves the result is a further reflection and subdivision. This again continues still further at the next impulse, so that finally, if the impulses can be kept up long enough, the result will be the division of the cord into four, five, six, and up to perhaps ten of these “ventral segments,” separated by nodes.

This being the mode of vibration of slow moving cords, we can see how the rapidly moving piano strings are instantly thrown into the state of complex vibration described above; for we must remember that not only is the vibration very rapid, ranging from 27 to more than 4100 vibrations per second, but also that there is no limit to the possible number of subdivisions. Moreover, the piano string is very stiff and being fixed at both ends and excited by a stiff blow, its motion is not only rapid but powerful, so that the reflections are unusually strong and numerous. Hence the wave of motion of the piano string is remarkably complex.

The entire complex motion of the piano string is of course the result of the operation of many forces, moving from different directions, upon a single resistance; so that the result of the interference of the forces with each other is that their net efficiency works out in some direction which is a resultant of all the directions. Thus, the piano string, if it be examined under motion by any optical method, is seen to vibrate in a wave motion which is the resultant of all the partial motions. The general appearance of such a wave is as shown in the illustration, figure 8, which gives (theoretically) the resultant of a wave motion including subdivision into six segments. The piano usually has the first eight and often the ninth, in the lower and middle registers, and still higher partials in the high treble, but the latter can hardly be isolated without special apparatus; and then not easily. Of course, as we shall see later, there are certain causes which affect the form of the wave in the piano string, in practical conditions, and so modify the series of partials.

One of the greatest of French mathematicians, Fourier, investigating another subject altogether, discovered the law of this harmonic motion of a string when he showed that every complex vibratory motion can be reduced to a series of simple pendular motions, of which the terms are as follows:

In other words, the very subdivision of the piano string into segments is here shown mathematically to be the necessary basis of all compound motion in vibrational form. Thus mathematics, from another angle, amply confirms the ideas above set forth.¹

The string, then, vibrates in its whole length, its 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8 and smaller segments indefinitely. The whole length vibration produces the fundamental tone of the string. The 1/2 gives twice as many vibrations, or the octave above. The 1/3 gives the twelfth, and the 1/4 gives the double octave. Thus, the piano string C 64, when sounded, actually involves not only the fundamental tone but all the following:

and many more not shown. All these are called partials. The fundamental is the first partial, the octave is the second, and so on. Above the tenth, although the number of possible subdivisions is unlimited, the pitch becomes less and less definitely referable to any specific note of the scale. The first 6 partials, as can be seen, are simply the common chord of C spread out. The 8th, 10th, 12th and 16th are octaves to the 4th, 5th, 6th and 8th. The 7th is flatter than the diatonic seventh which we use, although the former is the natural tone and the latter quite artificial.² The other odd-numbered partials are all more or less out of tune with their nominal equivalents, until, at a short distance above the 16th, all pretense of consonance except in the 20th, 24th and 32nd, has vanished.

It should be remembered that, although all the odd- and most of the even-numbered partials above the 10th are dissonant and this dissonance progressively increases — if one may use the term — the number of partials that may occur above the 10th in a piano string is quite large. This being the case, it will be understood that although these partials are relatively feeble, and their sounds do not affect the general sensation of pitch, they do have another effect; and this is felt in what is called the “quality” or “color” of the sound. In fact, as we shall soon see, the harshness or mellowness, thinness or fullness, of a sound, as evoked from the piano, not to mention the greater characteristic differences which distinguish the tone of one instrument from that of another, are all to be attributed to the manner in which the various partials are mixed with the fundamental.

But why should there be from one piano string a mixture of partial tones different from that which persists in another? For that matter, since the tendency of other sonorous bodies, like pipes for instance, is to divide up naturally into ventral segments, like strings, why should not all tone quality be alike? Obviously the difference must arise because one wave form varies from another ; or in other words because one string or pipe or rod produces one specific mixture of partials and another a different mixture. Why this should be so in the case of the piano string, which is our present concern, I shall now comprehensively explain, and the following discussion will be of great assistance in promoting an understanding of some most important problems.

The piano string is excited by a more or less violent blow from a felt-covered hammer. The impulse thus given to the string is relatively powerful, and its effect upon the highly tensioned filament of steel is such as to induce instant reflection of the sound-impulse and subdivision of the string into many ventral segments. But the exact individual segments into which the subdivision takes place are determined by one special condition; namely, by the position of the hammer 's point of contact. As will be remembered, the segments of the string are separated from each other by points of apparent rest called nodes. Of course, these nodes are not actually at rest, but the amplitude of their motion is greatly restricted by reason of the opposed forces pulling from each side upon them. If now the exciting blow is struck exactly on one of the nodes, the vibration of the shorter of the two segments into which that node divides the string, and equally the vibrations of all multiples thereof, are blotted out. Thus, if we wish to eliminate the 7th partial, we must strike on the 7th node, that is to say at exactly 1/7 of the string's speaking length. It is obvious that since the first six partials are simply components of the common chord of the fundamental or 1st partial, and the 8th is triple octave thereto, the elimination of the 7th will produce a perfectly harmonious flow of partials and in consequence a full round mellow tone. Experience confirms this deduction, although the exigencies of piano building usually compel a striking distance, as it is called, positioned at 1/8 or even higher for the greater number of the strings, and running progressively higher in the upper treble till it sometimes reaches 1/24 at the extreme C₇. The influence of contact point position is thus clearly shown, for if any of the very high strings be purposely struck at lower points than the hammers are fixed to strike them, it will be found that their tone is less bright, more mellow and even feebler. The last quality is due to the fact that the prime or 1st partial of these short stiff strings is not sufficiently powerful of itself and needs the backing, as one may say, of many partials to give it consistency and “ring.” It might be remembered incidentally that in the two highest octaves of the piano the progressively higher contact points of the hammers on the strings introduce series of partials running from the first ten to the first twenty. But the longer and more naturally powerful strings are struck at about 1/8 of their distance and would often be bettor off if struck at 1/7.

The properties of the material from which the string is made are also of importance in considering the precise nature of the mixture of partials which any given example may show. The stiffer a string is, other things being equal, the more rapid and complex will be the reflections of wave-motion and the consequent formation of ventral segments. By stiffness I do not mean thickness; for of course the thicker the string the less intense will be the wave-reflections and the fewer the high partials produced. But the piano is peculiar in that the tension of its strings does not vary largely from one end to the other, whilst the thickness does indeed differ very largely in proportion, since even in the understrung part of the scale the difference between the extreme treble and the first above the overstrung will usually be something like the difference between 5 and 8. So it follows that the upper treble strings are very much stiffer than those in the lower regions, in proportion to their length. Of course, the length factor enters into the complex here too, for the higher strings are shorter, and so again stiffer, for any given stretching force. Wire density. In the circumstances it would seem, after one has tested various pianos of various grades, that the idea of intensely hard wire is most distinctly a wrong idea; at least if we are trying to get round full tone and not hard glitter. The very hard wire is no longer so generally demanded, and piano makers are beginning to require a string of softer steel which shall tend to produce, under the lowered tension conditions thus made necessary, vibrational mixtures involving fewer ventral segments, the upper of which with their consequent partials shall be less prominent.

A softer wire cannot withstand excessive tensions. But we can easily see that high tension means stiffness, and one only has to listen critically to the tone of most pianos to realize that their strings do not err on the side of resiliency. They are usually too stiff as it is, and although the craze for clang and noise seems to be dying out — for which we should be thankful — still, there is much to be done yet. The piano of the future, let us hope, will be a low tension piano, equipped with softer wire and with a hammer shaped and positioned to kill the 7th harmonic and all its multiples ; a piano which will have few partials in its tone above the seventh and which in consequence will evoke sounds, full, mellow and sustained in quality.¹

In Chapter IX of this book, I make use of the material here set forth in order to show the practical application of Acoustical science to the work of tone-regulating or voicing pianos by manipulation of the hammer felt.

We shall now have to face the last and in some ways the most fascinating of all the subjects which we shall confront in the course of our examination into the vibrations of the piano string. So far we have confined our thought to individual strings sounding alone. We now have to consider the very beautiful and important phenomena arising from the sounding of two tones simultaneously. The inquiry is of the utmost importance in the higher analysis of piano tuning.

The piano serves us again to good purpose in examining the behavior of simultaneously sounded tones. Let us damp off one string in a triple unison on the piano. (All strings of the modern piano above the overstrung section are strung with three strings to the note.) This will leave two strings vibrating. If the piano has not been tuned very recently, it is almost certain that when we listen carefully to the sounding of these two strings we shall hear a sort of sound that can only be described as discontinuous and “wavy.”In order to make sure, suppose we choose the strings corresponding to C3 = 258.65 (middle C at international pitch). Let us damp one string of the triple and then slightly turn the pin of one of the others so as definitely to put it out of tune with its fellow. A very slight turn, just enough to feel the string give, will be sufficient. Now, take a tuning fork sounding exactly the same international pitch C₃= 258.65. Sound it, and listen carefully. You will hear a clear continuous tone, which persists without deviation or fluctuation. Put aside the tuning fork, strike the piano key, and listen. By contrast you hear a confused medley of sound, in which the fundamental pitch is discernible, but is surrounded by, and buried in, a mass of wavy, fluctuating, rising-and-falling sounds of a peculiar character, which are unmistakable when once heard. The peculiar character of these sounds is their rise-and-fall effect. The tone swells out far beyond its normal intensity and then dies away. This wave-like sound rises and falls at definite intervals, and it will be seen that the further apart in pitch the two strings are, the more of these rise-and-fall periods there will be in a given time. If now we begin to turn the tuning-pin backward, so as to bring the disturbed string again to its original equality of pitch with the other, we shall find that the wavy sounds gradually become slower and slower, until at length they disappear, and only the pure continuous tuning-fork tone remains; showing that the two strings have now been brought into perfect accord. Let us see what causes this interesting phenomenon.

We must go back for a few moments to some earlier considerations. A sound-wave is an oscillation to and fro. When a tuning fork prong vibrates, the first half of the vibration is when the prong moves away from its rest position and pushes the air in front of it against the surrounding air. This part of the vibration has the effect of compressing the air on that side, whilst on the other side the air moves forward to fill up the vacuum left by the moving away of the prong and thus is rarefied or thinned. Consider a vibrating pendulum (Fig. 10), and think of it as if it were a slow moving tuning fork. As the pendulum moves in one direction it condenses or compresses the air in front of it, and then as it moves back that same air is again rarefied or thinned out to its original density ; for air is elastic and rebounds. Thus each complete vibration of tuning-fork, string, or pendulum, no matter how slow or rapid, produces a condensation followed by a rarefaction of the surrounding air.

The space or distance between one condensation and the next, or between one rarefaction and the next, is called the wave-length. The more of these pulses there are in a second or other unit of time, the shorter the length of each. Sound travels at the rate of 1100 feet per second, roughly speaking — the wave-length of a tone of 100 vibrations per second therefore is 1100/100 or 11 feet. Figure 11 illustrates this point.

Thus we see that a sound-wave propagated through the air consists of a series of these oscillations of rarefaction and condensation. Now suppose that you start two such wave systems simultaneously from two strings perfectly in tune. Start them exactly at the same time so that the condensations begin together. A good example is the striking of two strings at once on the piano. The two run exactly together, condensation with condensation and rarefaction with rarefaction, as is shown by Figure 12, and are said to be in the same phase.

Now suppose we can arrange to start one string vibrating just half a complete vibration behind the other. Then condensation of No. 2 begins with the first rarefaction of No. 1 and we have the state of affairs pictured in Figure 13. Such a condition is called difference of phase.

Suppose two piano strings, one of which gives just one vibration less per second than the other. Now, when these two strings are sounded simultaneously, it follows that at the end of a whole second one will be exactly one vibration behind the other. Likewise at the end of half a second one will be half a vibration behind the other ; or in other words at the end of half a second, or right in the middle of one second's complete series of vibrations, the two will be in different phases, while at the end of a whole second they will have regained identity of phase; will be in the same phase together again. Suppose now we lay out on paper two wave systems, whose frequencies shall be in the ratio 8 : 9, for the sake of simplicity. Let us also show, by a third wave-curve, the result of the simultaneous activities of the two waves. In order to avoid a complex drawing I show just eight vibrations of the one and nine of the other. These will consequently begin and end together.

Now as soon as we examine these superimposed curves, we see that at the second complete vibration they are distinctly out of step with each other and by the time one has made four complete vibrations they are in definitely opposite phase. From this point onwards the difference subsides until at the eighth vibration of the one and the ninth of the other, the phase is again the same for both.

Now, it will at once be seen that when the two waves start, two condensations come together and so we have one condensation on top of the other, which of course means an increase in amplitude of the combined sound. Hence at the beginning of the waves the sound of the combined tones will be increased over the sound of either of them alone. We have a condition of resonance, as it is called.

On the other hand, when the middle of the curve has been reached we see that the condensation of one meets the rarefaction of the other exactly, so that at this point the one wave blots out the other and produces a perfect interference as it is called, canceling the sound altogether.

Hence we have the rise and fall of sound which we heard so clearly in the two piano strings mentioned above.¹ This rise and fall is very distinct and in the present case would occur at each 8-to-9 period; in other words, if the two waves were vibrating at 80 and 90 vibrations per second respectively, there would be heard 10 beats per sec,ond between them when sounded together.

Beats therefore arise between sounds nominally in unison but actually slightly out of tune with each other. The number of beats in a given time is equal to the difference between the frequencies of the generating tones.

Beats arise only between unisons. When heard in such intervals as the Octave, Fifth, Fourth, Third or others, this is because partial tones which may be common to both are thrown out of tune slightly ; and the beats arise between them. For instance, the beats in an octave which is somewhat out of tune arise between the prime of the upper tone and the second of the lower; which are the same. Example: C₁ = 64 and C₂ = 128. Prime of the higher is 128. Second of the lower is 128. These are therefore coincident, and if the strings which produce the primes are not in accord, the coincident partials will generate beats as above. The same is true in the interval of a perfect Fifth where the coincident partials are the 2nd of the higher and the 3rd of the lower. Please observe that the coincident partials always bear the same numbers as express the ratio of the fundamentals. Thus octave ratio = 1:2 and coincident partials are 2 and 1. Fifth ratio ==2:3 and coincident partials are 3 and 2. Fourth ratio = 3:4, and coincident partials are 4 and 3; and so on for all other intervals. For instance: Suppose one tone = 200 and another = 301. The interval is a Fifth, slightly out of tune, as the higher should be 300. Coincident partials are 3d lower and 2d higher. 200 X 3 = 600 ; 301 X 2 = 602. 602 — 600 = 2 = number of beats per second in this out-of-tune Fifth.

From what I have said, it becomes plain that the tuner will find beats very useful and must devote himself to practicing the art of hearing them and counting them. For it is evident that if the number of beats between any two coincident partials is equal to tlie difference between the frequencies thereof, then if we calculate the exact required frequency of each of the two members of an interval and from this calculate the frequency of their lowest coincident partials, we can easily and at once take the difference between the two latter, and whatever this difference be, that number of beats per second will be heard between them when sounded together. Therefore if we tune the two members of the interval so that we hear just that number of beats per second between them, we have tuned correctly. It then remains only to calculate these true values for the different tones of the piano and thus to establish proper beat-rates everywhere.

There is nothing unusual in all this really, for of course all tuners tune by counting beats, whether they call the process by this name or another. The point I am making here is that this process is the proper and natural process and that it is capable of being established mathematically, as has been done by Mr. J. C. Miller of Lincoln, Neb.; whose researches I am happy to be able to make use of in this book, as will be seen later.

We have now discussed to such an extent as is necessary for our present purposes the behavior of piano strings in vibration ; and have discovered that this discussion, if properly understood, is found to give us all needed assistance in both tuning and voicing, provided we can calculate the necessary frequencies of the tones required on the piano. We already know¹ that the piano does not permit pure tuning of the diatonic scale but that a system of compromise must be adopted to accommodate the inequalities of the diatonic scale to the unyielding 12 keys of the piano's octave. The system of Temperament used for this purpose, called the Equal Temperament, is now so firmly ingrained in practice that it is in fact the real basis of all modern music; rather than the diatonic scale, which indeed is now little more han an artificial abstraction. Of this, however, I shall speak in the next chapter.

If the present chapter has seemed at all involved this is only because I have had to treat an involved subject in simple language and small space. Still, all I have said here has been necessary and forms part of the argument which I am developing as to a system of piano tuning and tone-regulating; based on science and not on guesses or rule-of-thumb — and a good deal easier than if it were so based. For, indeed, among all the ridiculous superstitions of the human mind, none is either commoner or more absurd than that which covers with contempt the efforts of pioneers to formulate and apply scientific method. In truth, to do things scientifically is always to do them in the easiest as well as the best, way; and your “practical man,” untainted with one touch of theory, wastes time and energy in equal proportion.

1 Incidentally, let me say that the piano is an almost complete ready-made acoustical instrument for the investigation of the phenomena of musical strings, sympathetic resonance, beats and beat-tones, and partials. With a piano at hand the student can dispense with all experimental means except the tuning-fork. I shall suppose that a piano is at hand during the reading of this and other chapters.

1 For a further discussion of sympathetic resonance, see Chapter VII.

1 For discussions of this point, see my "Theory and Practice

of Pianoforte Building," Chapter VIII.

1 J. B. Fourier, 1768-1830, author of "Analysis of Determinate Equations."

2 Cf. Chapter 1, “Natural Scale.”

1 Other piano string characteristics: For some special cases exhibited by piano strings under practical conditions, the reader may consult Chapter VII. Piano bass strings: The special cases exhibited by the covered strings for the bass tones, are discussed in Chapter VII.

1See section on beats earlier in this chapter

YOU CAN NOW ORDER BY PHONE

BASS WIRE (Strings)

Online help available

Chapter II. ON THE VIBRATION OF A PIANO STRING. (TABLE OF CONTENTS)